It's discouraging that books and articles on navigation often
call for hundreds (if not thousands) of dollars' worth of electronic
gear, complicated formulae, and three-decimal place accuracy.
Happily, most of this stuff is simply unnecessary for navigating
small craft. In fact, you may end up with a better "feel"
for where you are and where you are going than when you read your
longitude and latitude on an LCD display. This is not to say that
electronic navigation aids can't be helpful and fun, but personally,
I'd rather spend the money on a bigger boat
or a longer sailing vacation. After all, Captain Joshua Slocum
sailed around the world with nothing more than an alarm clock,
a barometer, and a sextant. You won't need the sextant unless
you're going offshore, and "Cap" Slocum's clock was
missing one hand!
If you're like me, you'll probably be sitting on a corner of
the chart to keep it from flying overboard, with the sheet in
your teeth and the boat plunging about, and you'll be needing
the course now! Hence, your navigation aids should be impervious
to rain and spray and should be simple enough to use while holding
the tiller with one hand.
Speed, Distance, Time
One of the most basic navigation problems is knowing how far you've
gone, or how far you have to go. I made up a nomograph (commonly
found in applied engineering handbooks) that can solve any speed,
distance, time problem with speeds from 1/4 to 48 knots and times
from 5 minutes to 24 hours. I call it Gerr's Nomograph (below).
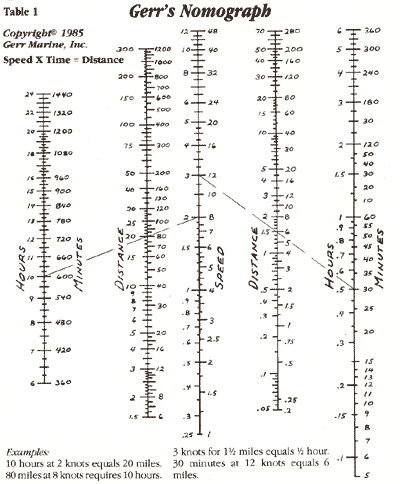
click for larger version
It was a chore to make up, but it's a dream to use. All you
do is lay a straight-edge from your speed to the time you have
been running and read your distance off the appropriate distance
scale.
Actually, Gerr's Nomograph is four nomographs in one. The right
hand side solves problems from 5 minutes to 6 hours, and the left
side solves problems from 6 lo 24 hours. The speed scale in the
center is numbered from 74 to 12 knots on the left and from 1
knot to 48 knots on the right. Accordingly, the distance scales
are numbered for the lower speed range on their left sides and
the higher speed range on their right. A bit of practice will
enable you to read the proper scale for your problem and to read
the numbering increments on that scale. Covered with clear contact
paper, it will be impervious to dampness.
Table 2 |
Wavelength
vs. Speed |
Knots |
Wavelength |
| .5 |
1.5 in. |
.75 |
4 in. |
| 1 |
6 in. |
2 |
2.25 ft. |
| 3 |
5 ft. |
4 |
9 ft. |
| 5 |
14 ft. |
6 |
20 ft. |
| 7 |
27 ft. |
8 |
36 ft. |
| 9 |
45 ft. |
10 |
50 ft. |
| 11 |
67 ft. |
12 |
80 ft. |
Multiply knots by 1.15 to get miles per
hour. Multiply miles per hour by .87 to get knots. At
.25 knots there are barely discernable ripples.
|
You can determine any one variable if you know the other two.
Thus, you can find time if you know speed and distance; distance
if you know speed and time; and speed if you know distance and
time. Another nice feature of the nomograph is that you can get
alternate solutions for a desired course, great for planning cruises.
It works for either knots or miles per hour. If you enter knots
in the speed column, then your distance answers will be in nautical
miles (6,080 feet). If you enter mph, then your distance answers
will be in statute miles (5280 feet)
How Fast Are You Going?
Most people look at their knotmeter, stream a log over the stem,
or stick a "wand" in the water to determine how fast
their boat is going. But you needn't do any of this. All you have
to do is glance over the side for a moment.
Most sailors know that a displacement hull's top speed is equal
to 1.34 times the square root of the boat's waterline length.
That is because water makes surface waves of precise lengths depending
on how fast your boat is going. This is very convenient for judging
speed (Table 2). It's also a good way to estimate how fast the
"other guy" is going, as it's simple to see the wave
pattern along his hull. (You do have to have some idea how long
his boat is, though.)
For navigation purposes, however, the important thing is the
large difference between the wavelengths at different speeds.
You will have little difficulty telling the difference between
the 1/2 foot wave lengths of one knot and the 2-1/4-foot wave
lengths of two knots. Discount spurious waves that are kicked
up by plunging and turbulence. With a little practice and common
sense you will soon be an expert at making speed estimates to
a quarter of a knot.

Copy scales directly from your most used charts
- Two on each face - Place widely differing scales on the dsame
face to avoid confusion - Cover both faces with clear contact
paper and coat all with clear floor wax or varnish (click image
for larger version
The Distance Rule
Once you can tell how fast you're going and can solve
speed, distance, time problems, you can plot and lay off courses
on your chart with a simple distance rule you can make yourself
(Fig 1, above).Take a piece of white oaktag (heavyweight, smooth-surface
white cardboard), cut a strip around 12 to 16 inches long by l-1/2
inches wide, and carefully draw on the scales for four of your
most common chart sizes, copying directly from the legend on those
charts (two scales on one face and two on the other). Then, cover
both sides of the scale with clear contact paper and, finally,
a couple of coats of clear floorwax (good
clear varnish would also do nicely).
To lay off a course place the distance rule on the chart - making
sure you are using the correct scale - and draw a line between
where you are (starting point) and where you want to go (destination
point). Actually, you usually don't even need to draw a line,
just make a dot at the starting and destination points and read
the distance right off the rule. There's no clumsy stepping off
with dividers, you need only one hand, and it's very quick.
If you think there's a significant current running, mark the
destination point and then lay the distance rule from that point
in the direction exactly opposite to the current flow or set (Fig.
2, below). Current speed is called "drift," current
direction is called "set." Say you glance at a buoy
(or the tide and current tables) and estimate the drift at 3/4
knot and the set to be heading you at about 50 degrees on your
starboard bow. You see on the distance rule that the baseline
distance to your destination is 8 miles; and you know you're going
about 5 knots. From Gerr's Nomograph, you find that it'll take
just over 1-1/2 hours to go this course (8 miles devided by 5
knots = 1.6 hours). Using Gerr's Nomograph, you can also see that
the current will set you off about 1-1/8 miles (3/4 knots x 1-1/2
hours = 1-1/2 miles). Simply mark a dot (current point) at 1-1/8
miles in the direction opposite to the current flow (upstream)
from the destination point. Place the distance rule between the
current point and the starting point. This gives the course to
steer and the new distance, in this example, 8.8 miles. The new
time - 1 hour and 45 minutes - can be determined from Gerr's Nomograph
in a jiffy. To complete these steps only takes about 90 seconds.
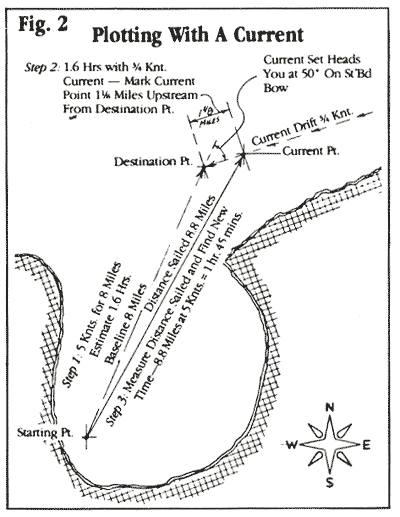
On your new course, you will appear to be aiming for the current
point (not your destination point), but because of the current,
your boat will actually be sliding sideways, so you will end up
at your original destination point. This system is not exactly
geometrically accurate, but how often have you been in a current
of perfectly constant speed and direction? If your course is particularly
long or if there are dangers nearby, then you must take additional
time to be more precise and be sure to stay well to weather of
any obstacles. Also keep in mind that the slower you're going,
the greater the relative effects of current set and drift. When
ghosting along in a fog, for instance, you certainly must take
special care with your calculations.
In practice, though, I've seldom found that I needed any more
accuracy than the above methods give. Bearing angles taken in
a small boat in a stiff breeze are always going to be off by a
degree or two (or more) because of the motion of the boat and
your closeness to the water. With so many variables, and conditions
so poor for taking bearings and getting fixes, you can't worry
about the decimal points. Get the big picture in nice round numbers,
and you'll always know where you are.
Next Month: A Homemade Tacking Computer.

|

