|
Bird’s
Mouth Spars
The Real Equations
By David Farless
|
|
Introduction
I recently became interested
in the Bird’s Mouth technique for hollow spar construction
after encountering web sites where the technique was being
applied. One of these is a site called Building
of Aslan (author/owner Frank Hagan) and the other is
an article in DuckWorks Magazine (A
Birdsmouth Mast for Skat by Dave Burdecki).
The Bird’s Mouth technique
for hollow spar construction uses 8 wooden staves of rectangular
cross section, each with a 90º notch cut in one edge.
The staves are glued together by nesting a corner of one
stave into the notch of the next stave. The Aslan web site
presents basic “rule-of-thumb” methods for calculating
the dimensions of the staves. The stave cross sectional
dimensions are arrived at by first dividing the desired
spar outside diameter (O.D.) by 2.5 to get the width of
the stave cross section and then setting the stave depth
at 1/2 of the width. The Aslan article cites WoodenBoat
Magazine (WoodenBoat, Number 149, July/August, 1999) as
the source of the rules-of-thumb.
I decided to order the back
issue of WoodenBoat to see the mathematics behind these
basic calculations. The article in WoodenBoat is “Bird’s
Mouth Hollow Spars”, by Aime´ Ontario Fraser.
Unfortunately, the only math presented is in a side-bar
titled Scantlings for Bird’s Mouth Spars which contains
two formulas. These formulas are:
stave width = 0.4 x O.D.
stave depth = 0.2 x O.D.
As expected, these formulas
match the rules-of-thumb used in the Aslan web site, since
multiplying by 0.4 is the same as dividing by 2.5 and 0.2
is half of 0.4.
These rules-of-thumb for
Bird’s Mouth spar development seem to work, but are
not supported by any hard analysis. The WoodenBoat article
ascribes them to a mysterious “retired engineer”
who passed them to two Connecticut boat builders (Craig
Wright and Richard Duke) and then disappeared.
Being a retired engineer
myself, I decided that I should be able to repeat the analysis
by which these rules-of-thumb were derived. What follows
here is that derivation.
The Geometry
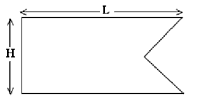 The cross-sectional shape of the staves for the Bird’s
Mouth spar is shown in this figure. The shape is a rectangle
of width L and depth H, with a 90º notch cut out of
one edge. The technique under discussion here uses 8 of
these staves to make an approximately circular spar section.
(More or fewer staves may be used, but this analysis only
considers the case of 8 staves.)
The cross-sectional shape of the staves for the Bird’s
Mouth spar is shown in this figure. The shape is a rectangle
of width L and depth H, with a 90º notch cut out of
one edge. The technique under discussion here uses 8 of
these staves to make an approximately circular spar section.
(More or fewer staves may be used, but this analysis only
considers the case of 8 staves.)
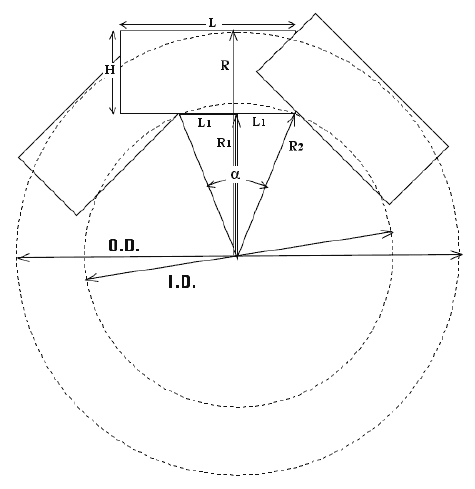
A cross section
of the resulting spar is shown below. (Only 3 of the 8 staves
are shown, for simplicity.) In this figure, R is the radius
corresponding to the outer diameter of the spar (O.D.),
R1 is the distance from the center of the spar to the inner
edge of the staves, and R2 in the radius corresponding to
the inner diameter of the spar (I.D.). Defining R2 as the
inner radius of the spar rather than R1 is a conservative
assumption (from the standpoint of strength) in that it
ignores the additional wood left inside of this circle (unless
the spar is reamed out to a circular inside diameter). |
The angle 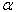 in this figure is just the full circle divided by the number
of staves; i.e.
in this figure is just the full circle divided by the number
of staves; i.e.
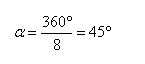
The Equations
Based on the desired O.D.
and I.D. of the spar, the dimensions of the stave cross
section may be calculated from the following equations:
Given O.D. and
I.D., calculate L and H,
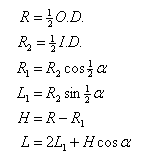
Alternatively, if slats of
a given cross section are to be used, the O.D. and I.D.
of the resulting spar can be calculated as follows:
Given L and H,
calculate O.D. and I.D.
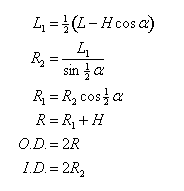
Additional parameters
of interest.

|
Mass is proportional to the cross-sectional
area of the spar. Strength is proportional to the moment of inertia
of the cross-section of the spar. For a clear, entry-level discussion
of relative mass and strength for hollow spars, see Jim
Michalak’s discussion of hollow spars in his newsletter
from February 2000.
 The
Calculated Results The
Calculated Results
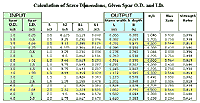
The table at right (click to enlarge)
shows the results of these calculations for spars with O.D. of
1, 2, 3, and 4inches and with varying I.D. values.
After using the WoodenBoat article
rules-of- thumb
to calculate stave dimensions for spars with O.D. of 1, 2, 3,
and 4 inches, the second set of formulas was used to calculate
the actual resulting spar diameters. The next table shows the
results. (click to enlarge) thumb
to calculate stave dimensions for spars with O.D. of 1, 2, 3,
and 4 inches, the second set of formulas was used to calculate
the actual resulting spar diameters. The next table shows the
results. (click to enlarge)
The Analysis
Note in the first table that for
all spar O.D. values, if the ratio H/L is 0.500 (see entries highlighted
in yellow) then the mass relative to a solid spar is always 56
% and the strength is always 81% of that for a solid spar. This
is also shown in the second table where L and H have been selected
in all four calculations by using the rules-of thumb as given
in WoodenBoat. The rules-of-thumb are said to provide stave dimensions
giving spars with an O.D. of 1, 2, 3, and 4 inches. However, the
actual spar O.D. is always 2.4% high or about 1/16 inch for a
3-inch spar. This error of less than 1/16 inch for spars of less
than 3-inch O.D. is well within acceptable error for small boat
builders.
I have not tried to verify the
wall thickness needed to meet accepted scantlings for wooden boat
spars. However, the WoodenBoat article quotes the Connecticut
boat builders (Wright and Duke) as saying that “the formula
to determine the thickness of the staves perfectly matches the
recommendations for hollow round masts in Skene’s Elements
of Yacht Design by Francis S. Kinney.” The Connecticut
builders are further quoted in the WoodenBoat article, as follows:
| “Wright and Duke feel that this formula results in
an excessive wall thickness for small-craft masts and is more
appropriate for larger yachts having spars of spruce. Their
experience has proven that you can make the thickness as little
as 0.10 times the major diameter for very small, light boats.
They use a factor of 0.15 for clear Douglas fir, since it
is stronger than spruce in every way.” |
So, it seems safe, and perhaps
overly conservative, to apply these rules-of-thumb for development
of hollow wooden spars for small boats.
The Summary
This analysis supports the use
of the mysterious engineer’s rules-of-thumb for Bird’s
Mouth spar development as presented in WoodenBoat. He had obviously
“done his work” well as spars resulting from the use
of his rules-of-thumb will result in a circular spar very near
the intended dimensions and with more than adequate strength for
small boats. And they will give a reduction in spar weight of
about 44% while retaining 81% of the strength of a solid spar.
(A 62% improvement in the strength-to-weight ratio!)
Given that the “Rules-of-Thumb”
can provide reasonable and useable stave dimensions, the equations
presented here may seem to be over-kill and unnecessary. However,
they can be useful in at least two situations. First, they can
be used to determine how much to taper the staves (reduction in
L) to achieve a given O.D. at the end of a tapered spar. Second,
they can be used to calculate the inside diameter resulting from
given stave dimensions, allowing estimates to be made of the strength
and mass of the spar.
And, perhaps most importantly,
they provide a documented basis to support knowledgeable use of
the rules-of-thumb.
|

