BOAT
BUILDING WITH A DIFFERENCE IX
(For Aspiring Amateurs)
by Barend Migchelsen
LOOKING BACK
When America was “discovered”,
there were only two native hull designs: the canoe and the kayak.
By themselves, marvels of the “art” of design, and
the “craft” of construction.
On the east coast, all the other
boat designs are the result of the know-how of European emigrants:
English, Scottish, French (St.-Pierre), Dutch, and German (Lunenburg).
According to the guru of
American Small Boat Building, the late John Gardner, dories were
developed from constant-flared, straight-planked double-enders
of which the sheers had a “natural” bend. See page
43 in The DORYBOOK.
The definition of a “natural”
bend is: “part of a circle arc,” or a “circle
segment.”
Originally the sheer line
of the double-ender was a circle segment. The “tombstone”
stern which made the double-ender a dory, came in later. Also
later came the varying flare, the straightening out of the sheers
aft, and fore which resulted in a steeper, nearly straight curve
in the bow, and a change from “biscuit” shape to “cod’s-head,
mackerel-tail” form.
Each design is a compromise.
The first compromise is
the ratio LOA/Beam. By making a hull wider, you will gain more
stability and loading space. You will loose streamlining which
slows the boat down.
Making the hull narrower
will result in less room; the hull becomes “tender”,
or less stable. It reduce the water resistance.
Boats were built long before
people learned writing, drawing, and math in schools. Ages of
experience taught the first, illiterate builders that for double-enders
the best compromise between Length Overall and Beam is LOA/Beam
= 4/1.
To put it in figures: measured
inside, a double-ender with a LOA of 16 feet should be 4 feet
wide at Beam. If you stick to this ratio, for small boats you
don’t have to make any other calculations.
 When
the tombstone stern was brought in, the double-ender became a
dory. It shortened also the LOA to 15½ feet. That is were
the odd sizes come in. When
the tombstone stern was brought in, the double-ender became a
dory. It shortened also the LOA to 15½ feet. That is were
the odd sizes come in.
Another thing is that East
Coasters have the habit to either calling the length of a dory
by the length of the waterline in the USA, or by the length of
the bottom in Canada.
If called by the length
of the bottom (Lunenburg), the actual Overall length is 7 feet
for what is called a 5-foot Dory. Subsequently a 12-foot Dory
has an actual Length Overall of 15' 6".
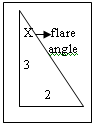 Back
to flare. The first double-enders were constant flared. That flare
angle was, and still is, 33 degrees, 41 minutes, 24.24 seconds
(33º 41' 24.24"). Back
to flare. The first double-enders were constant flared. That flare
angle was, and still is, 33 degrees, 41 minutes, 24.24 seconds
(33º 41' 24.24").
It sounds crazy. But
it is NOT!
Look at the flare as the
hypotenuse of a right triangle. Make the ratio between the short,
opposite leg and the long, adjacent leg 2/3. You get this odd-looking
angle figure of 33 degrees, 41 minutes, 24.24 seconds.
LIKE THE 3, 4,
5 CARPENTER’S TRIANGLE, THE 2/3 RATIO ITSELF IS A MARVEL
OF SIMPLICITY!
This ratio is nothing new.
It is the “maximum” flare figure that is
found in many European designs, much older than the dories, like
the Dutch farmer’s punters (about 500 years). The punters
were the most basically designed simple double-enders: two wide,
thick side planks set on a bottom formed as a biscuit.
When you check the (official)
drawings of the most typical “Lovell” dory at Beam,
you will find that exact flare angle ratio. So is it in the Dory
model-kit from Wind and Waves, from Dartmouth, Nova Scotia,
marketed at Can$29.95.
A 16-foot. Double-ender
with dory flare, made with straight side planks, produces a rather
excessive bottom rocker.
Experience taught the fisherman,
and subsequently the builders, that this was not good for a sea-boat.
It produces too much seesawing. To reduce the rocker in the bottom,
an extra partial strake, a stealer, was put in fore and aft.
At least in Lunenburg, east
coast dories have a reduced rocker of only approximately three
inches between Beam and bow.
Next development: the flare
ratio produces a very strong curve in the bow stem.
By straightening out the
sheer line fore, the bowline became steeper, and the curve was
reduced. It made it easier to cut the stem from the tough, curved
root stumps of Hackmatack trees. The bevel of the stem became
less varying, more constant. It gave more buoyancy fore.
This is where the “cod’s
head” came into the design. It gives more room over the
bottom fore without changing the overall length of the hull, or
the curvature of the sheer lines.
The most difficult, time-consuming
part of double-ender construction is making the stems fore and
aft. First, because they were made of tough-to-work hackmatack
root stumps, second, the cutting of the correct form is not easy,
even if you have a good template. The reason is that the bevel
angle of the sides of the stem is not constant.
Replacing one of the two
stems, the stern stem with a triangular transom board, the “tombstone”,
saved a lot of time and effort. The double-ender became a dory.
The tombstone has the form of a V, which is very simple and quick
to make from the easier-to-work-with cedar wood.
By allowing the side panels to go free (straight) aft from the
last setup frame as the tangent to the sheer line circle segment,
the bevel of the sides of the V-transom became constant, another
time saving improvement.
Dories have no rudder. By
making a cutout for an oar in the top edge of the tombstone, it
became possible to steer and/or scull the boat.
It seems only a very small
improvement, but for the lonely fisherman it could mean the difference
between life and death. If he had lost or broken an oar, now he
could scull back to the schooner, or, in case of inland fishing,
get back to the shore instead of drifting out into the ocean with
an outgoing current.
Replacing the stern stem
with a tombstone, and making the sheer line straight after the
last setup frame, resulted in a slightly longer, narrower bottom
aft: the “mackerel tail” of the “cod’s
head, mackerel tail” shape of the bottom. This effect is
greatly enhanced by increasing the height of the side panels and
bow fore. The chines no longer run parallel to the sheer
but their lines are converging towards Beam.
Dories are open boats. With
the loose cross benches removed, they can be stacked eight to
twelve boats high aboard a schooner. Before WW2, the schooner/mother-ships
sailed to the Grand Banks. The purpose of the dories was not
to be sailed, or rowed, but to provide a safe fishing platform
to which the (cod) lines could be anchored.
The side panels were made
very wide, 26 to 30 inches for a 15½ ft. hull. This served
dual purposes: The deep hulls could hold a big load of fish. The
crew could lean safely against the side without having to be afraid
of falling overboard while working the lines. Falling overboard
was disastrous because most fishermen could not swim, besides
having little chance in the often rough, chilly waves with their
heavy clothing of two or three sets of longjohns under their heavy
flannel shirts and corduroy pants, rain gear, and high rubber
boots. They fished within hailing distance of the mother ship
that often was invisible in the frequent, heavy fogs.
The windage factor of the
high sides was not important. Once the fishing lines were out,
the boats were stationary. As mentioned before, their only purpose
was to provide a safe fishing platform. The beautiful, eye-catching
shape of the dory was not important, except for riding the waves
extremely well in their anchored-to-the-lines positions in, most-of-the-times,
rough swells. They needed no skeg, no keel. Some had a small mast
with a spritsail aboard. With that set up, and no keel, or even
a skeg, they drift quite a bit to lee. It did not matter, the
distances to the schooner were short, and there was plenty of
room in the ocean.
They also (mistakenly) believed
that a shot of rum helped protect them against the relentless-penetrating,
cold and damp climate, which could be seen in the discoloring
of their faces: bluenoses.
There used to be quite a
few rumrunners that had their home bases in one of the many, difficult-to-patrol
inlets of the Nova-Scotia east coast. The schooner captains bought
the rum directly at sea from these runners.
Now you understand why the
queen of the schooner fleet carried that name. Most East-Coasters
have a good sense for humor.
Odyssey
If you have gotten the impression
that I was trying to show you how to build a Dory, then I have
given you the wrong idea.
What I am writing about
is that how the Odyssey of 20 years slow, and often frustrating
research if the lines of hard-chined, constant-flared hulls were
based on simple mathematics that were easy to understand for aspiring
amateurs, and get them started into building, succeeded. It resulted
in a system that would allow any person who had completed
the math of grade eight of secondary school, and is interested,
to design, loft and construct his own hull from double-ender,
dory, skiff, punt, dinghy to pram, with any amount of flare.
To do this, no higher
mathematics, the trial-by-error guesswork of conical development,
or expensive software of Computer Aided Design (CAD) is needed!
But, it does require an
open mind, especially from the experienced builders that
have never done, or seen it done that way. Just refresh what
you learned about the Theorem of Pythagoras.
Once an aspiring amateur
has succeeded with his first boat, in 90 percent of the time,
he is hooked. Nothing will stop him, or her anymore.
So, now you can never
say that you were not warned before you start giving in to that
contagious urge of building your own boat.
Over that 20-year period,
I have measured and tried to analyze the lines of every hard-chined
hull I could lay my hands on, discussed, and often debated that
issue.
Since those hulls were mainly
dories and dory wrecks, it explains how they were so often mentioned
until now. From this moment on, I will be talking only about double-enders
and how you can develop other hull shapes from this basic boat.
Lunenburg
I have married children,
grandchildren, and a sister-in-law living near Halifax, N.S. During
our twice-yearly visits, I started to checkout boat builders in
that area, and tried to ask questions.
 Kim
Smith is the proprietor of the Dory Shop at the very end of the
Lunenburg waterside. He is a builder who really knows what he
is doing, and has thought a lot about design. Kim
Smith is the proprietor of the Dory Shop at the very end of the
Lunenburg waterside. He is a builder who really knows what he
is doing, and has thought a lot about design.
One day I asked him: “Kim,
how do you design your dories?’
The answer was: “I
never did. I have a bottom and a stem template, and a set of frames
for every one of the 11 sizes that are built here, hanging on
the walls. All I do is to set them up and plank them.”
Next questions: “Where
do these frames come from? Who made them?”
Kim: “I don’t
know. The shop has been here since the early 1900s. After the
shop had been closed for a few years, I was asked to open it up
again. The frames were hanging on the wall. Since they are tried,
and proven to produce beautiful dories, all I do is set them up
and start planking.”
It suddenly dawned on me,
why I never got the right answers. Many of the old timers had
learned how to set them up and do the planking, but had never
bothered to ask further questions. In their heydays, especially
before WW2, they made good living planking the set-up frames,
and for nearly all of them the rest was of no interest.
They could never have done
that without set-up frames.
Eureka
In 1990, after rereading
John Gardner’s DORYBOOK that phrase on page 43
started to hitch in my (rusty) brain box: Sheer line, “natural”
bend. But after 15 years, I had not come one step further.
In the summer of 1991, I
had an accident. In the dark, I fell in an uncovered basement
hole. I landed on a concrete floor, seven feet lower, with one
broken, and one cracked pelvis bone.
In the hospital bed beside
me was a cabinetmaker with a locked shoulder. He was reading a
woodcraft magazine; I read the last issued WoodenBoat Magazine.
When we were finished, we
switched literature. And there it was, the mathematics of a circle
segment on a chord with the utterly simple calculation of the
relationship of the (maximum) height of the circle arc to the
length of the chord, and the radius of the circle.
I had just turned 70 in
1991, and all what I had learned in grade 8 of the secondary school
56 years earlier, and that had been forgotten, came back to me
in that week in the hospital bed.
John Gardner’s remark
about the connection between the sheer line of a double-ender,
and a circle arc segment had indeed pointed me in the right direction.
The solutions jumped at me right from that magazine page.
I have reproduced that drawing.
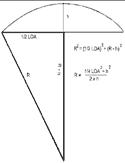 If you are like me, a long time behind this stuff, that drawing
will help to refresh your (rusty) memories
If you are like me, a long time behind this stuff, that drawing
will help to refresh your (rusty) memories
Above all, keep this drawing in mind for the first five written
articles of this series. You will see how this diagram relates,
and is the key to a set of drawing plans for a constant-flared,
hard-chined double-enders.
In the here-reproduced drawing,
(click to enlarge) note that:
R = the radius of the circle arc
h = the (maximum) height of this segment on the chord
R - h = the distance between the chord and the center point.
In the right angled triangle, the long, adjacent leg = R - h.
The short, opposite leg = ½ length of the chord
The hypotenuse of the triangle = the radius R.
Apply the theorem of Pythagoras:

Worked out the answer is:
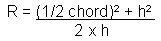
I am a Dutch emigrant who came
in 1959 to Canada. My only mathematical knowledge is what I learned
in secondary school between 1933 and 1939. That is a long time
ago.
After three years of learning
to adapt to our new homeland, as most beginning immigrants, I
earned not enough to live, but just enough not to starve. I became
a life insurance agent working on commission. That is a love-hate
affair: Every Monday morning you start from square one. Even when
you have sold a policy, you still don’t know if the client
will pass a medical exam. You bite your nails for another week
to ten days. If the medical examiner turns him, or her down, you
have lost it.
To work off my frustrations, in
1975, I took up boat building as a hobby. I built a 16-foot Frisian
scow with leeboards (See page 229- Boatbuilding by Chapelle
for a 22-ft. illustration). In the Netherlands they make them
with oak planks, heavy workboats. Mine was built from ¼"
ply. Quite a difference.
Notwithstanding that she was a
lot lighter, the boat sailed terrifically and to my surprise was
very stable and had a perfect balance. Call it “beginners
luck.”
After having built two, or three
more hard-chined hulls, I began to suspect that hard-chined designs
were based on a few, simple, straightforward mathematical theorems.
How could I find that out? Where to start?
On trips to these cities, I went
to all the public libraries from Toronto, Ottawa, Montreal, and
Halifax. Researched in the boating section # 623 all what was
available on the subject “Building”. In the mean time,
I also tried to keep up with the magazine publications in North
America, England, and Holland. I bought some of the books (if
I could afford them).
All that literature gives many
details, but never a simple, mathematical answer.
But why, with so many plans around,
pursue this at all?
Here are the reasons:
If my suspicions were correct,
finding the solutions meant that, at least, I had mastered the
theory. Then, I only had to bring up the practical part to par.
After all, I had no training, or schooling in that direction.
I did not have the time, or the money to get one. Like many of
you who read Duckworks Magazine, I was only an aspiring amateur
dreamer of building boats.
But there were other considerations
too: For an amateur, the ideal place for building a boat is under
a carport. But the wintry climate of Canada and many states of
the USA makes that impossible for at least six month of the year,
sometimes longer, depending on where you live. It forces the amateur
builder into hibernation for that part of the year. With mathematics
you can prefab the smaller parts precisely in a small place indoors,
a kind of constructing your own building kit, and assemble the
hull outside as soon as the weather allows it. That way you get
a head start on the season. What a trade school would take two
years to teach you in theory, could be done by reading at home
in a couple of weeks and by making a to-scale model from inexpensive
cardboard on the kitchen table. The building of the model turned
out slightly more difficult than the real thing because of the
smaller tolerances and the inferior (paper) material. It gives
perfect “hands-on” training that costs next to nothing.
It shows you all the difficulties that turn up in building the
full-sized model, and then some.
Before WW2, having a secondary
school leaving certificate was not for everybody. That changed
drastically after WW2. Today everybody must have that piece of
paper. It is only the first rung on the career ladder.
That means that today everybody who is at least 15-years old,
knows the basic math of the theorem of Pythagoras and the (basic)
definitions of the trigonometric ratios of sine, cosine, and tangent.
If, at his time, John Gardner,
who had a college education, had worked that out practically,
he would have had very few people he could tell it to. As was
the custom in those years, most boat builders got only an elementary
school education. Because of the economic conditions, quite a
few of them never completed their elementary schooling. Today
everybody has learned the simple math in secondary school.
The hard-chined dory is developed
from a constant-flared double-ender by replacing the stern stem
with a triangular transom board. It only changes the design in
so far that the LOA became ½ to ¾ foot shorter.

A hard-chined Dory-Skiff is developed
from the double-ender by lopping ¼ of the LOA aft, and
plugging the hole with a transom board. That makes the ration
LOA/Beam change from 4/1 to 3/1. There is no change to
the shape of the chine and sheer lines, or in the shape of the
bow. Beam lies then at 2/3 of LOA.
A Punt is a Dory-Skiff of which
1 to1½ foot of the bow is cut off. The hole is plugged
with a (bow) board.
In other words: The mathematics
not only show you how to build one boat, but the whole range of
hard-chine hulls from double-enders to prams, without having a
buy a new set of plans for each model.
It has become a system.
Here comes another little gem.
The flare (angle) of hard-chined,
small-boat hulls can vary between zero degrees (no flare) to maximum
flare = dory flare =33 degrees, 41 minutes, 24 seconds = 2/3 ratio.
For a 16-foot double-ender with
dory flare that means a sheer line half-Breath at Beam of 24",
and a Profile height of 16". Please take note of these figures.
You can find and check them with the tables in BBwaD
III of this series.
For convenience, most hard-chined
small boat designs have a flare (angle) that falls between 6 degrees
and 30 degrees.
By starting to play with the flare
ratio figures, an amateur who has digested the mathematics and
understands them, can design his own hard-chined, small-boat hull
between 1-ft. LOA to 30-ft. LOA, with a flare between 0 degrees
to maximum (dory) flare, over the whole range of hull types: from
double-ender to prams as is shown in the two tables of BBwaD III.
For example, the ratio 10/24 gives a flare angle of 22.62 degrees
= 22 degrees, 37 minutes, 12 seconds. Another difficult figure,
but an easy template setting: A right triangle with a
long leg of 12", and a short leg of 5".
It is no longer a question of
buying a plan and attaching batten A to frame B. Any “planker”
can do that. It has become a complete understanding of design,
lofting, and construction, the what, the why, and the how of a
series of hard-chined, small-boat hulls.
You won’t need a PC
with expensive software. No higher mathematics. No trial-by-error
conical development.
All that you need, and what today
every interested amateur has, although he, or she, may have to
refresh that because it was a long time ago that you learned it,
is what you were taught in grade 8 of secondary school: the theorem
of Pythagoras, and the (basic) definitions of the trigonometrically
ratios Sine, Cosine, and Tangent that are found on a secondary-school
pocket calculator. You can always ask any teenager of 15-years
and older to help you. They will be delighted to bring you up
to date (again).
What I have written here might
upset a lot of professionals who make a living by selling the
expensive software, the plans, and books that will tell you that
you can build a canoe in 6 (six) hours, or a skiff in 8 (eight)
hours. I am sorry to say that there is not, or that there ever
will be such a thing as an “instant” boat short from
buying one.
If you are an aspiring amateur
builder and dream of building your own boat, be prepared that
the construction of the hull is only 1/3 (one-third) of the job.
Finishing, and painting are the other two 1/3 parts.
Sheers and chines, Barend.
If you have missed any of the preceding articles
of the Boat Building with a Difference look up the name “migchelsen”
on the web. You can retrieve the whole series from there.
|

