|
Technical
Drawings
Usually, a set of technical drawings consists of a Body view, a Profile view and a
Plan view. The Plan view is
sometimes called the “Seagulls’ view”.
The Plan view is divided by the longitudinal centerline into two
halves that are each other’s mirror image.
For that reason the drawing can be simplified to an illustration
of one side on the centerline. It
is called the half-Breadth view. See
figure 2-1.
Once
you become familiar with and accustomed to the “set of plans”, it is
easy to forget that they are nothing else than projections that often give a
complete different, sometimes distorted picture from the reality.
To give an extremely striking example:
A straight line in a Profile and half- Breadth view can show up
as just a single dot in the Body view, i.e., the center line.
Only by looking at the first two illustrations do we become aware
that the dot in the Body view represents a full straight line.
Another example is that a circle can show up as a
straight line in two projection planes.
Only the third projection will give us the real picture.
Plans
of a Double-Ender
Figure 2-1 shows the three projection drawings of a
16-ft. Double-Ender with constant flare.
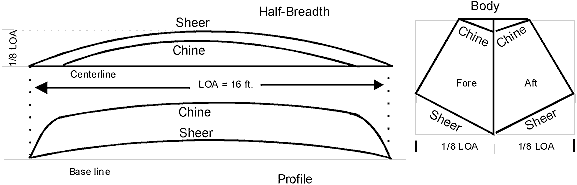
Fig. 2 - 1
Set of plans of
a Double-Ender
In de Half-Breadth and Profile view the sheer lines
show up as parts of elliptical curves.
In the Body view that sheer line is a straight line!
Also, the sheer line in the Body view is the
hypotenuse of a right triangle. That
right triangle conforms to the other right triangle above it on the side.
The hypotenuse of this second right triangle is the side panel of
the hull. The angle between the long leg and the hypotenuse of that right triangle
represents the constant flare angle
of the side panel.
In the right triangle of which the sheer line is the
hypotenuse, the horizontal (long) leg represents the width
of the half-Breadth at Beam in the half-Breadth view. This width is
1/8 LOA =
24".
The vertical (short) leg of this triangle is the Profile height at Beam in the Profile view.
IF that Profile
height is 10",
the hypotenuse/sheer line is 26" according to the theorem of Pythagoras (a2
= b2 + c2).
The late John Gardner states on page 43 in The
Dory Book that the sheer line of the Double-Ender is a “natural
curve”. By definition
that means “part of a circle
(arc).”
A chord is a straight line on which a circle arc
stand. The half-Breadth view shows us clearly that chord.
It is the centerline of the drawing.
The length of the chord = the length of the centerline = the
Overall Length: LOA =16 ft. = 192"
To
draw the real sheer line has now become the grade-8, secondary school,
mathematical problem how to draw a circle arc on a chord when you know the
length of the chord, and the height of the arc above the chord.
Rephrased, the real question is: Calculate the
radius of a circle arc standing on a chord.
The chord is 192", the height of the arc is 26".
I
obtained my high school certificate in 1939.
Since that time, all that I had ever used from all the mathematics
that I had crammed in high school was Ohm’s Law, which is expressed by
the formula V = I x R. I
had needed the formula to figure out the rating to replace a blown-out
Xmas-tree light in a series string. My
knowledge of mathematics had stifled, and rusted over in a far away corner
of the brain box. I searched
some old school books that my by-this-time-married children had left
behind. But having learned
mathematics in Holland, I had a hard time with the expressions of the
English language equivalents in 1990, 50 years later.
I experienced one of the very few moments that I felt lost.
An
accidental fall into a seven-feet deep hole landed me on a concrete
basement floor and subsequently in the hospital with a broken Ischium
bone. In the other bed was a
cabinetmaker with a locked shoulder.
He
read a woodworker’s magazine. I
was reading WoodenBoats. Hospital days are very long, especially if you are not real
sick. The next day we
switched magazines. On page 4
was the solution of my problem. All
you need is to apply the Pythagorean equation.
See figure 2-2. The
applicable numbers are already put in
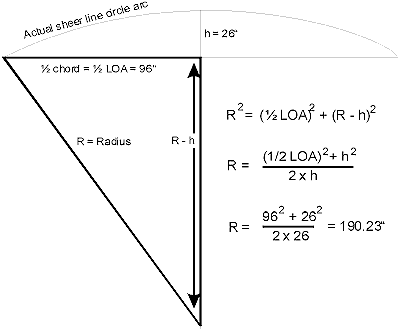
Fig. 2 - 2
Radius of a
circle arc segment on a chord
THE
KEY
Do
I hear the question: Now that
you can calculate the radius of the sheer line circle arc, SO
WHAT? …
In the month that I was forced to sit out the healing
of my broken bone, I discovered that once I knew the radius of the sheer
line, it is easy to figure out:
1.
The height of the arc at each station. That
determines the exact location of
the station lines in the Body
view. They can be drawn in
into figure 2-1. See figure
2-3.
2.
Once you do that, all the values of the Profile heights and
half-Breadth at the stations are at your fingertips.
You can compile the offset table of the hull lines
3. The exact real bevel
angles of the cross frames
and the transom.
4. The width at
each station, and the total length
of the expanded side panels
5. The length, the
shape, the rake, and the crosscut angle
of the (bow) stem).
6. The measurement
and the shape of the bottom.
What
is more important: It was no
longer necessary to calculate any of these figures.
A full-sized Body view drawing reveals all this information.
Take off the measurement with a dividers compass.
Transfer them to the building material directly.
A method that is far more accurate and certainly faster than
measuring with a ruler and loft the hull from the offset table.
Profile and half-Breadth drawings have become redundant.
Offset tables, often a primary cause of troubles, are no longer
needed.
A successful project starts with an accurate
technical drawing.
My technical drawings are reduced to a circle arc on
a chord, and a right triangle.
You can’t go far wrong with that, or improve the
degree of accuracy! Even if
the drawings are scaled down to the easy to handle size of ¼, a high
degree of accuracy can be achieved. On
top of that, IF
you know how to use the Staedtler-Mars scale (ruler) #987 18-34 and make
the drawing on one-inch-grid graph paper, you can use the same figures
from the full-sized illustration.
No conversion calculations, not the slightest
chance of making mistakes. Practically,
a foolproof method.
My
“SET OF PLANS” for The Double-Ender
Figure 2-3A and B are just that.
In figure 2-3B, the locations of the station lines are plotted onto
the hypotenuse. Since the
vertical middle line divides the drawing into two mirror-image-equal
halves only one half is drawn, just as the half-Breadth drawing replaces a
full Plan view illustration.
In figure 2-3B the long, 24",
horizontal leg of the right triangle is the half-Breadth at Beam.
The vertical, 10",
short
leg is the Profile height at Beam.
The 26" hypotenuse represents hn
= hBeam = h8.
For clarity, only the locations of the even-numbered
station lines are plotted on the hypotenuse. Besides that, more frames are seldom necessary.
If
both drawing are made on one-inch-grid graph paper, the numbers of the
offset tables can be “read-off” from the drawing.
As mentioned before, it is a lot quicker and more
accurate to transfer the dimensions to the material with a dividers
compass. Good bye and good
riddance offset tables!
If any of the readers can shows me a better, faster,
and more accurate way, IMHO, I think, we all like to hear about that.
The drawings also make a Profile and a half-Breadth
view redundant, be it with one definite
and one possible exception.
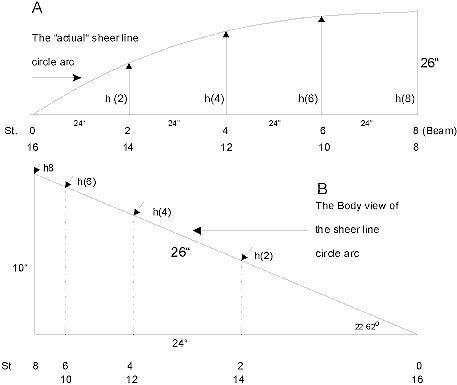
Fig. 2 - 3.
Actual sheer line circle arc (A)
Body view of the sheer line arc (B)
Note:
The drawing A and B are made to scale.
However, for clarity, the scale of drawing B is 4 times the scale
of drawing A
The
Exceptions: Bow stem and
Transom
The real
shape of the bow stem can be
seen only in the Profile view.
Also, if the hull has a raked transom, its real length and rake
angle only show up in the Profile view.
Before
this is explored, you have to get acquainted with a couple of other short cuts that facilitate building a hard-chined hull.
That will be shown and discussed later.
Cross
Frame Bevel Angles
To obtain the maximum “bearing” surface for a
good connection to the side panels, the side edges of the cross frames and
the frame linings are beveled. See
figure 2-4. A skilled
carpenter has no difficulty with that.
If it does not fit perfectly, a couple of strokes with a plane, et
voila´.
Plywood edges and narrow lining battens are difficult
to plane. Beginning amateurs
usually don’t have good carpenter’s skills.
I should know, because I don’t have them still.
But the skill is not necessary.
The bevels are easily cut with a table saw.
Never take the
bevels from the half- Breadth view. They
are always wrong.
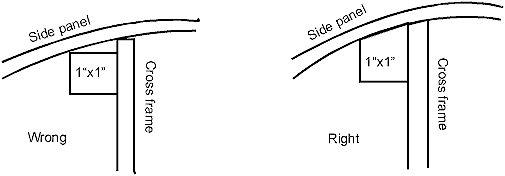
Fig. 2 - 4
Side panel
“bearing” on cross frame
A
bevel angle of a cross frame is equal to the center point angle between
the radius of that particular station and the radius at Beam. See figure 2-5.
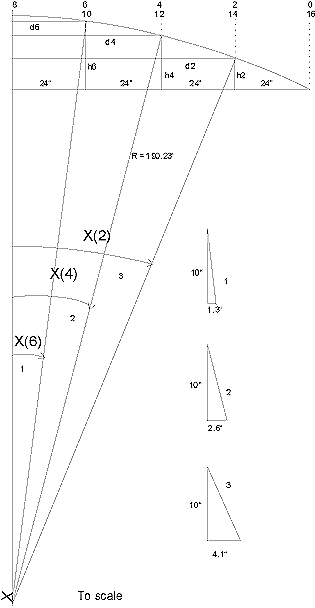
Fig 2 - 5
The cross frame
bevel angles are equal to the center point angles
The sine of the center point angle X4 is Sin angle X4 = d4/R = 48/190.23 = 0.252326. The angle X4
= 14.615º. In the same way, Sin
angle X2 = d2/R = 72/190.23 = 0.3785. The angle X2 = 22.24º, and Sin
angle X6 = d6/R = 24/190.23 = 0.126. The angle X6 = 7.25º
The pleasant thing is that you don’t need to do
any calculation! Transfer the
size of each center point angle of the actual circle arc drawing to a
triangular piece of scrap plywood as shown in the drawing.
Place that right-triangular template with its short leg on the
table. Tilt the saw against
the hypotenuse. The bevel
cuts will be “dead on”. Cutting
the templates goes faster than making the calculation.
Mark
the templates clearly, because they are needed for #10 frame (= #6), #12
frame (= #4), and #14 frame
(= #2). That way, the bevel angles of the corresponding frames are
perfectly equal.
Sheers
and Chines, Barend. |
![]()